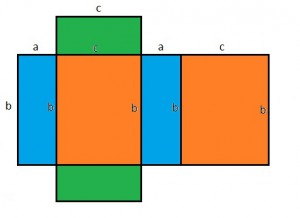
Aby obliczyć pole powierzchni prostopadłościanu, należy „rozebrać” go na części. Na rysunku obok mamy przedstawioną siatkę prostopadłościanu o trzech wymiarach (a, b, c). Jeśli się dobrze przyjrzeć, zauważymy, że prostokąty o jednakowym kolorze mają takie same wymiary:
Prostokąt niebieski ma wymiary a • b
Prostokąt zielony ma wymiary a • c
Prostokąt pomarańczowy ma wymiary b • c
Ponieważ każdy z nich jest przedstawiony dwa razy, to pole na przykład prostokątów niebieskich będzie wynosiło: P = 2 • a •b (w skrócie P = 2ab). Jeśli dołożymy do tego pola pozostałych prostokątów, to otrzymamy pole całej bryły
P = 2ab + 2ac + 2bc (na kolorowo zaznaczyłem poszczególne prostokąty z rysunku)
Pole prostopadłościanu
P = 2ab + 2 ac + 2bc