Funkcja to jedno z najważniejszych zagadnień w matematyce. Na poziomie gimnazjalnym jest ona dosyć prosta i intuicyjna.
Funkcją nazywamy przyporządkowanie każdemu elementowi z jednego zbioru dokładnie jednego elementu z drugiego zbioru.
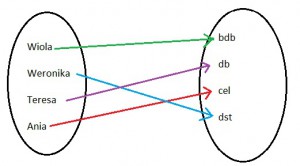
Rozważmy pierwszy zbiór, w którym mamy uczennice klasy 2 gimnazjum, oraz drugi zbiór, w którym mamy poszczególne oceny. Jak widać każdemu elementowi z pierwszego zbioru (element w pierwszym zbiorze to każda z dziewczyn), został przyporządkowany dokładnie jeden element z drugiego zbioru. Takie przyporządkowanie możemy nazwać funkcją.
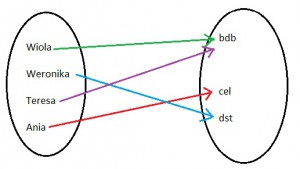
Załóżmy jednak, że dziewczyny dostały inne oceny:
Jak widać Teresa tym razem dostała ocenę bdb. Czy to przyporządkowanie możemy nazwać funkcją? Oczywiście, że tak, ponieważ nadal spełniony jest wymóg, że każdemu elementowi z pierwszego zbioru odpowiada element z drugiego zbioru. Nie ma znaczenia, że zarówno dla Wioli jak i Teresy element jest ten sam.
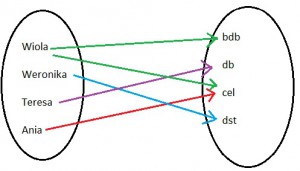
Poniżej kolejny przykład. Czy tym razem mamy do czynienia z funkcją?
W tym przypadku nie możemy mówić o funkcji, gdyż jednemu elementowi z pierwszego zbioru zostały przyporządkowane dwie wartości.
I jeszcze jedna zagadka. Czy tym razem mamy do czynienia z funkcją?
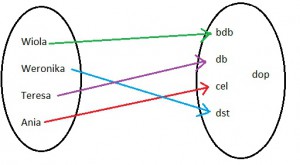To przyporządkowanie jak najbardziej jest funkcją. Jeden element z pierwszego zbioru jest przyporządkowany do dokładnie jednego elementu z drugiego zbioru. Nie jest ważne, że nie wszystkie elementy z drugiego zbioru zostały „użyte”.
INNY SPOSÓB PRZEDSTAWIANIA FUNKCJI
Funkcję można przedstawić również w tabelce. Weźmy ostatni przykład.
Zamiast rysować zbiory, można w tabelce przyporządkować poszczególnym dziewczynom konkretne oceny.
ZADANIA