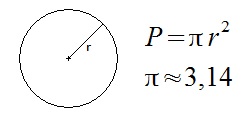Zanim pochylimy się nad wzorem na pole koła wyjaśnię po trochu różnicę między kołem a okręgiem.
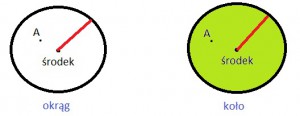
Patrząc na powyższe rysunki przychodzi na myśl zabawa „znajdź różnice”. Z rysunku widzimy, że okrąg tworzą tylko punkty wyznaczone przez promień (kolor czerwony), leżące w równej odległości od środka okręgu. Od razu więc widzimy, że punkt A nie należy do okręgu. Jak sytuacja wygląda w przypadku koła? Do koła należą wszystkie punkty oddalone równo z długością promienia oraz te, które leżą bliżej niż długość promienia (zaznaczone na zielono). Punkt A zatem jest częścią koła.
Podsumowując jednym zdaniem: okrąg to brzeg koła, nie ma zatem pola, tylko długość. Koło natomiast jest wycinkiem płaszczyzny, więc musi mieć jakieś pole.
Wzór na pole koła
π – czytamy jako „pi” jest to stała wielkość w matematyce, w przybliżeniu wynosząca 3,14; r to oczywiście długość promienia koła. Pole koła jest więc równe iloczynowi liczby π z drugą potęgą długości promienia.