Na liczbach całkowitych wykonujemy działania identyczne, co na naturalnych, czyli dodawanie, odejmowanie, mnożenie, dzielenie, itp. Jednak ze względu na to, że czasami mamy do czynienia z sytuacją gdy jedna z liczb jest dodatnia, a druga ujemna, sprawy zaczynają się nam nieco komplikować. Spróbuję nieco przybliżyć te zagadnienia:
Dodawanie liczb całkowitych:
I przypadek – obie liczby są dodatnie
Sytuacja bardzo prosta, dodawanie wykonujemy identycznie jak przy liczbach naturalnych, np.
4 + 7 = 11
II przypadek – pierwsza liczba jest dodatnia, a druga ujemna
Jeśli pierwsza liczba ma większą wartość bezwzględną niż druga (lub równą), to dodawanie po prostu zamieniamy na odejmowanie i obliczamy, np:
8 + (-3) = 8 – 3 = 5 albo 7 + (-7) = 7 – 7 = 0
Jeśli pierwsza liczba ma mniejszą wartość bezwzględną niż druga, wtedy od drugiej odejmujemy pierwszą, a wynik zapisujemy ze znakiem „-„, np:
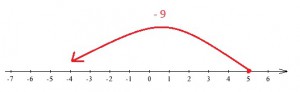
5 + (-9) = 9 – 5 = 4 => do wyniku dopisujemy znak ujemności zatem działanie ma wynik – 4
Możemy to przedstawić również na osi liczbowej:
Naszym miejscem początkowym jest liczba 5. Ponieważ mamy dodać liczbę ujemną, to tak naprawdę odejmujemy 9. „Startując” z liczby 5 przesuwamy się o 9 miejsc w lewo i „lądujemy” na -4
III przypadek – pierwsza liczba jest ujemna, a druga dodatnia
Jeśli wartość bezwzględna pierwszej liczby jest większa niż wartość bezwzględna drugiej liczby, wtedy odejmujemy wartości bezwzględne tych liczb, a do wyniku dopisujemy minusa.
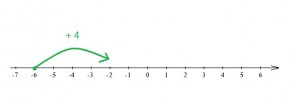
– 6 + 4 = – 2 (ponieważ 6 – 4 = 2, i musimy dopisać minusa do wyniku)
Na osi liczbowej przedstawilibyśmy to następująco:
„Startujemy” z liczby – 6. Ponieważ mamy dodać 4, to przesuwamy się o 4 miejsca w prawo i „lądujemy” na -2.
Jeśli obie liczby mają takie same wartości bezwzględne to wynik wynosi 0, np:
– 7 + 7 = 0
Jeśli wartość bezwzględna drugiej liczby jest większa niż wartość bezwzględna pierwszej, wówczas od drugiej liczby odejmujemy pierwszą
– 2 + 9 = 7 (ponieważ 9 – 2 = 7)
IV przypadek – obie liczby są ujemne
Jeśli obie liczby są ujemne, wówczas dodajemy te liczby, a do wyniku dopisujemy „-„, np:
– 6 + (-3) = -9 (bo 6 + 3 = 9, i dopisujemy do dziewiątki znak ujemności)
ZADANIE