Na liczbach całkowitych wykonujemy działania identyczne, co na naturalnych, czyli dodawanie, odejmowanie, mnożenie, dzielenie, itp. Jednak ze względu na to, że czasami mamy do czynienia z sytuacją gdy jedna z liczb jest dodatnia, a druga ujemna, sprawy zaczynają się nam nieco komplikować. Spróbuję nieco przybliżyć te zagadnienia:
Odejmowanie liczb całkowitych:
I przypadek – obie liczby są dodatnie
Jeśli pierwsza liczba jest większa od drugiej (lub równa), wówczas odejmujemy identycznie jak przy liczbach naturalnych, np:
9 – 2 = 7 albo 8 – 8 = 0
Jeśli druga liczba jest większa od pierwszej, wówczas od większej z nich odejmujemy mniejszą, a do wyniku dopisujemy znak minus, np:
3 – 8 = – 5 (ponieważ 8 – 3 = 5 a do wyniku mieliśmy dopisać znak ujemności).
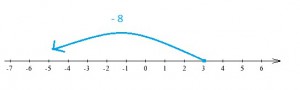
Na osi liczbowej przedstawiamy to w ten sposób:
„Startujemy” z liczby 3, a następnie przesuwamy się o 8 miejsc w lewo i „lądujemy” na -5.
II przypadek – pierwsza liczba jest dodatnia, a druga ujemna
W takim wypadku odejmowanie zamieniamy na dodawanie (w myśl zasady, że minus i minus dają plus), np:
5 – (-4) = 5 + 4 = 9 (na różowo zaznaczone dwa minusy, które „zamieniają się” w plusa). Nie ma tutaj znaczenia, czy pierwsza liczba jest większa, czy druga.
III przypadek – pierwsza liczba jest ujemna, a druga dodatnia
Dodajemy wartości bezwzględne tych liczb, a do wyniku dopisujemy minusa, np:
– 2 – 3 = – 5 (ponieważ 2 + 3 = 5, i do wyniku dopisujemy znak ujemności). Nie ma tutaj znaczenia, czy pierwsza liczba jest większa czy druga.
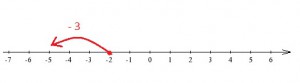
Na osi liczbowej wygląda to tak:
Zaczynamy od liczby -2 i przesuwamy się o 3 miejsca w lewo, kończąc na – 5.
IV przypadek – obie liczby są ujemne
Stosujemy zasadę „minus i minus dają plusa”, a następnie postępujemy tak samo, jak przy dodawaniu liczb całkowitych, np:
– 5 -(-2) = – 5 + 2 = – 3 albo – 7 – (-8) = – 7 + 8 = 1
ZADANIE